BZOJ3684: 大朋友和多叉树

Description#

我们的大朋友很喜欢计算机科学，而且尤其喜欢多叉树。对于一棵带有正整数点权的有根多叉树，如果它满足这样的性质，我们的大朋友就会将其称作神犇的：点权为1的结点是叶子结点；对于任一点权大于1的结点u，u的孩子数目deg[u]属于集合D，且u的点权等于这些孩子结点的点权之和。给出一个整数s，你能求出根节点权值为s的神犇多叉树的个数吗？请参照样例以更好的理解什么样的两棵多叉树会被视为不同的。我们只需要知道答案关于950009857（453*2^21+1，一个质数）取模后的值。

Input#

第一行有2个整数s,m。第二行有m个互异的整数，d[1],d[2],…,d[m]，为集合D中的元素。

Output#

输出一行仅一个整数，表示答案模950009857的值。

Sample Input#

4 2
2 3

Sample Output#

HINT#

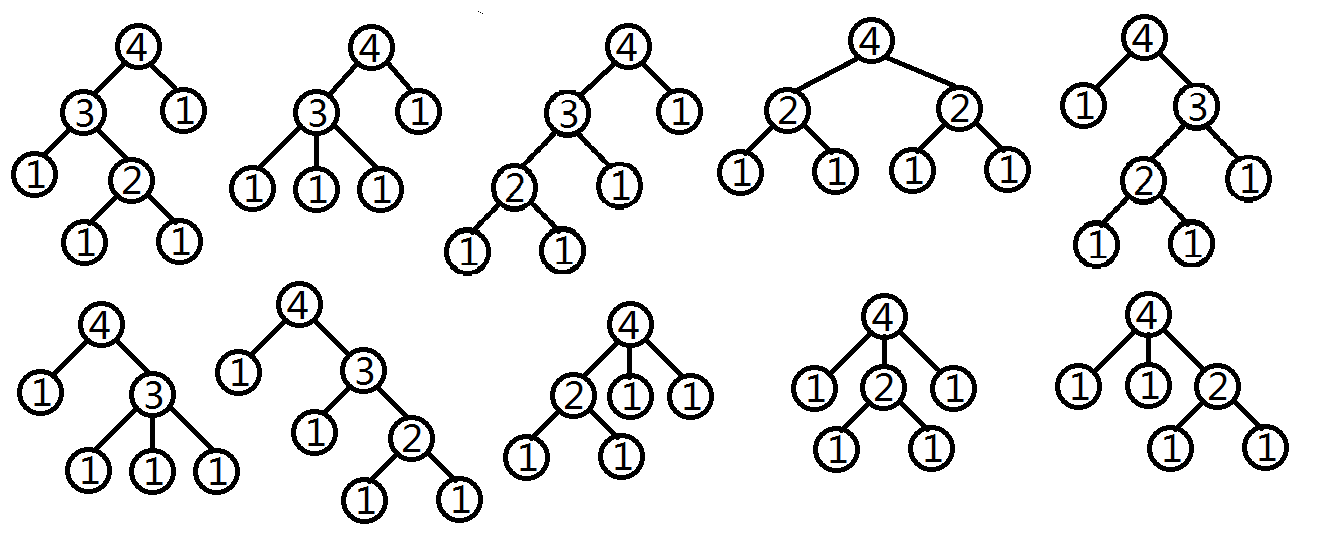
数据规模： $1 \leq m < s \leq 10^5$ , $2 \leq d[i] \leq s$ ，有3组小数据和3组大数据。

题解#

求出树的生成函数 $T(x) = \sum_{i\ge 0} t_ix^i$ $T(x) = x + \sum_{k \in S}T(x)^k$

移一下项 $T(x) - \sum_{k \in S}T(x)^k = x$

设 $G(y) = y - \sum_{k \in S}{y^k}$

$x = G(T(x))$

$T(x)$ 为 $G(x)$ 的复合逆

上拉格朗日反演

$[x^n]T(x) = \frac{1}{n}[x^{n-1}] ( \frac {x}{G(x)} )^n$

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 950009857;
const int MAXN = 2e6 + 5;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
long long pow_mod(long long a, int b)
{
    long long ans = 1;
    while (b)
    {
        if (b & 1) ans = ans * a % MOD;
        b >>= 1;
        a = a * a % MOD;
    }
    return ans;
}
int rev[MAXN];
int Inv;
void FFt(int *a, int N, int op)
{
    int w, wn, t;
    for (int i = 1; i < N; i++)
        if (i < rev[i])
            swap(a[i], a[rev[i]]);
    for (int k = 2; k <= N; k <<= 1)
    {
        wn = pow_mod(7, op == 1 ? (MOD - 1) / k : MOD - 1 - (MOD - 1) / k);
        for (int j = 0; j < N; j += k)
        {
            w = 1;
            for (int i = 0; i < (k >> 1); i++, w = 1ll * w * wn % MOD)
            {
                t = 1ll * a[i + j + (k >> 1)] * w % MOD;
                a[i + j + (k >> 1)] = (a[i + j] - t + MOD) % MOD;
                a[i + j] = (a[i + j] + t) % MOD;
            }
        }
    }
    if (op == -1)
        for (int i = 0; i < N; i++)
            a[i] = 1ll * a[i] * Inv % MOD;
}
int tmp[MAXN];
void Get_Inv(int dep, int *a, int *b)
{
    if (dep == 1) return b[0] = pow_mod(a[0], MOD - 2), void();
    Get_Inv((dep + 1) >> 1, a, b);
    int N = 1;
    while (N < (dep << 1))
        N <<= 1;
    Inv = pow_mod(N, MOD - 2);
    for (int i = 1; i < N; i++)
        if (i & 1)
            rev[i] = (rev[i >> 1] >> 1) | (N >> 1);
        else
            rev[i] = (rev[i >> 1] >> 1);
    //copy(a, a + dep, tmp);
    for (int i = 0; i < dep; i++)
        tmp[i] = a[i];
    for (int i = dep; i < N; i++)
        tmp[i] = 0;
    //fill(tmp + dep, tmp + N, 0);
    FFt(tmp, N, 1);
    FFt(b, N, 1);
    for (int i = 0; i < N; i++)
        b[i] = 1ll * b[i] * ((2 - 1ll * b[i] * tmp[i] % MOD + MOD) % MOD) % MOD;
    FFt(b, N, -1);
    for (int i = dep; i < N; i++)
        b[i] = 0;
    //fill(b + dep, b + N, 0);
}
int G[MAXN], Ans[MAXN], C[MAXN];
int main()
{
    int n = read(), m = read();
    C[0] = 1;
    for (int i = 1; i <= m; i++)
        C[read() - 1] = MOD - 1;
    Get_Inv(n, C, G);
    Ans[0] = 1;
    int b = n;
    int N = 1;
    while (N < 2 * n)
        N <<= 1;
    Inv = pow_mod(N, MOD - 2);
    for (int i = 1; i < N; i++)
        if (i & 1)
            rev[i] = (rev[i >> 1] >> 1) | (N >> 1);
        else
            rev[i] = (rev[i >> 1] >> 1);
    while (b)
    {
        if (b & 1)
        {
            FFt(Ans, N, 1);
            FFt(G, N, 1);
            for (int i = 0; i < N; i++) Ans[i] = 1ll * Ans[i] * G[i] % MOD;
            FFt(Ans, N, -1);
            FFt(G, N, -1);
            for (int i = n; i < N; i++)
                Ans[i] = 0;
        }
        b >>= 1;
        FFt(G, N, 1);
        for (int i = 0; i < N; i++) G[i] = 1ll * G[i] * G[i] % MOD;
        FFt(G, N, -1);
        for (int i = n; i < N; i++)
            G[i] = 0;
        // fill(G + n, G + N, 0);
    }
    printf ("%d\n", 1ll * Ans[n - 1] * pow_mod(n, MOD - 2) % MOD);
}