Description#

给出n个数qi，给出Fj的定义如下：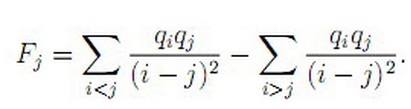
令Ei=Fi/qi，求Ei.

Input#

第一行一个整数n。
接下来n行每行输入一个数，第i行表示qi。
n≤100000，0<qi<1000000000

Output#

n行，第i行输出Ei。与标准答案误差不超过1e-2即可。

Sample Input#

5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880

Sample Output#

-16838672.693
3439.793
7509018.566
4595686.886
10903040.872

题解#

写写题解证明自己还活着

这道题是一道比较基础的题目

先把Ei写出来得

$E_i = \sum_{i<j} {\frac{p_i}{(i - j) ^ 2}} - \sum_{i>j}{\frac{qi}{(i - j)^2}}$

令 $f(i) = q_i,\ g(i) = \frac{1}{i^2}$

$E_j=\sum_{i=1}^{j-1}f(i) \times g(j-i)-\sum_{i=j+1}^nf(i) \times g(j-i)$

前一部分直接FFT算。

后一部分$\sum_{i=j+1}^nf(i) \times g(j-i)=\sum_{i=1}^{n-j}f(i+j) \times g(i)$

令 $f'(n-i-j)=f(i+j)$ ，则第二部分变为 $\sum_{i=0}^{n-j-1}f'(n-i-j-1) \times g(i)$，转化为卷积的形式用FFT解即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <complex>
using namespace std;
#define Complex complex<double>
const double pi = acos(-1.);
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int MAXN = 100005 * 8;
int rev[MAXN]; 
double Inv;
int N;
void FFt(Complex *a, int op)
{
    Complex t, w;
    for (int i = 0; i < N; i++)
        if (i > rev[i]) swap(a[i], a[rev[i]]);
    for (int k = 2; k <= N; k <<= 1)
    {
        Complex wn(cos(pi / (k >> 1)), op * sin(pi / (k >> 1)));
        for (int j = 0; j < N; j += k)
        {
            w = Complex(1, 0);
            for (int i = 0; i < (k >> 1); i++, w = w * wn)
            {
                t = a[i + j + (k >> 1)] * w;
                a[i + j + (k >> 1)] = a[i + j] - t;
                a[i + j] = a[i + j] + t;
            }
        }
    }
    if (op == -1)
        for (int i = 0; i < N; i++)
            a[i] *= Inv;
}
Complex a[MAXN], b[MAXN], g[MAXN];
int main()
{
    int n = read();
    n--;
    for (int i = 0; i <= n; i++)
    {
        double x;
        scanf ("%lf", &x);
        b[n - i] = a[i] = x;
    }
    for (int i = 1; i <= n; i++) g[i] = (1. / i / i);
    int m = n + n + 1;
    N = 1;
    while (N < m)
        N <<= 1;
    Inv = 1. / N;
    for (int i = 0; i < N; i++)
        if (i & 1)
            rev[i] = (rev[i >> 1] >> 1) | (N >> 1);
        else
            rev[i] = (rev[i >> 1] >> 1);
    FFt(a, 1), FFt(b, 1), FFt(g, 1);
    for (int i = 0; i < N; i++) a[i] = a[i] * g[i];
    for (int i = 0; i < N; i++) b[i] = b[i] * g[i];
    FFt(a, -1), FFt(b, -1);
    for (int i = 0; i <= n; i++)
        printf ("%.3f\n", a[i].real() - b[n - i].real());
    // while (1);
}