Description#

Input#

Output#

Sample Input & Output#

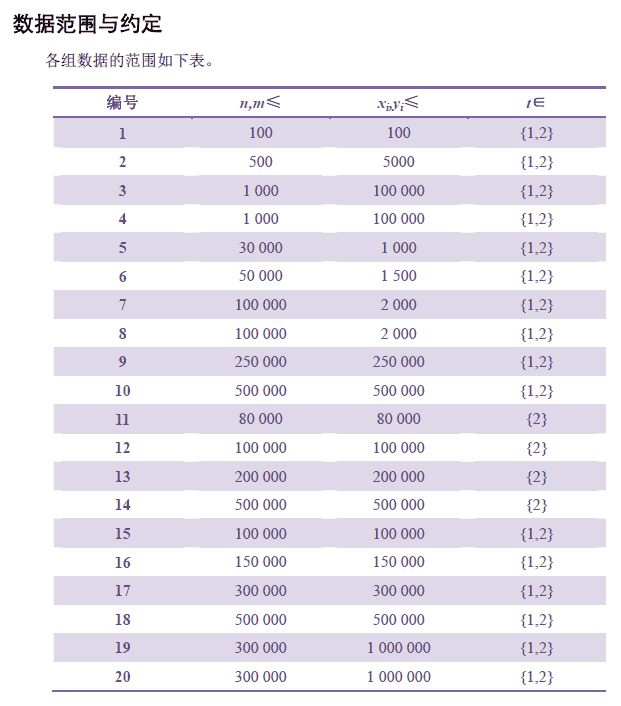
HINT#

题解#

KD-Tree带插入的板子。
应该rebuild的。
但没rebuild就过了。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

const int INF = 0x3f3f3f3f;
const double alpha = 0.756;
const int MAXN = 5e5 + 5;

int now;

struct Point
{
    int d[2];
    int &operator[](const int &x)
    {
        return d[x];
    }
    inline bool operator < (const Point &x) const 
    {
        return d[now] == x.d[now] ? d[now ^ 1] < x.d[now ^ 1] : d[now] < x.d[now];
    }
}a[MAXN], cur;

#define dis(_, __) (\
    int(abs(_[0] - __[0]) + abs(_[1] - __[1]))\
)

#define size(_) ((_) ? (_)->s : 0)

struct Node
{
    Node *ch[2];
    Point v;
    int s, d;
    int Max[2], Min[2];
    Node(Point x)
    {
        ch[0] = ch[1] = NULL;
        v = x;
        s = 1, d = now;
        Max[0] = Min[0] = x[0];
        Max[1] = Min[1] = x[1];
    }
    Node(){;}
    inline bool operator < (const Node &x) const 
    {
        return v < x.v;
    }
    bool IsBad()
    {
        return ((size(ch[0]) > s * alpha) || (size(ch[1]) > s * alpha));
    }
    void Pushup(Node *x)
    {
        if (!x) return;
        for (int i = 0; i <= 1; i++) Min[i] = min(Min[i], x->Min[i]);
        for (int i = 0; i <= 1; i++) Max[i] = max(Max[i], x->Max[i]);
        s += x->s;
    }
    int min_dis()
    {
        int ans = 0;
        ans += max(Min[0] - cur[0], 0) + max(cur[0] - Max[0], 0);
        ans += max(Min[1] - cur[1], 0) + max(cur[1] - Max[1], 0);
        return ans;
    }
}*root;

inline void Build(Node *&rt, int l, int r, int d = 0)
{
    if (l > r) return;
    int mid = l + r >> 1;
    now = d;
    nth_element(a + l, a + mid, a + r + 1);
    rt = new Node(a[mid]);
    Build(rt->ch[0], l, mid - 1, d ^ 1);
    Build(rt->ch[1], mid + 1, r, d ^ 1);
    rt->s = 1;
    rt->Pushup(rt->ch[0]);
    rt->Pushup(rt->ch[1]);
}

Node **res;

inline void Insert(Node *&rt)
{
    if (rt == NULL)
    {
        rt = new Node(cur);
        res = NULL;
        return;
    }
    now = rt->d;
    if (cur < rt->v) Insert(rt->ch[0]);
    else Insert(rt->ch[1]);
    rt->s = 1;
    rt->Pushup(rt->ch[0]);
    rt->Pushup(rt->ch[1]);
    if (rt->IsBad()) res = &rt;
}


inline void Insert(Point x)
{
    cur = x;
    Insert(root);
}

int Min_ans;

inline void Query(Node *rt)
{
    if (!rt) return;
    // if (rt->min_dis() > Min_ans) return;
    Min_ans = min(Min_ans, dis(rt->v, cur));
    int dis_l = rt->ch[0] ? rt->ch[0]->min_dis() : INF;
    int dis_r = rt->ch[1] ? rt->ch[1]->min_dis() : INF;
    if (dis_l < dis_r)
    {
        Query(rt->ch[0]);
        if (dis_r < Min_ans) Query(rt->ch[1]);
    }
    else
    {
        Query(rt->ch[1]);
        if (dis_l < Min_ans) Query(rt->ch[0]);
    }
}

inline int Query(Point x)
{
    cur = x;
    Min_ans = INF;
    Query(root);
    return Min_ans;
}

int main()
{
    // freopen("1.in", "r", stdin);
    // freopen("2.out", "w", stdout);
    int n, m;
    n = read(), m = read();
    for (int i = 1; i <= n; i++)
        a[i][0] = read(), a[i][1] = read();
    Build(root, 1, n);
    Point x;
    while (m--)
    {
        int t = read();
        if (t == 1)
        {
            x[0] = read(), x[1] = read();
            Insert(x);
        }
        else
        {
            x[0] = read(), x[1] = read();
            printf ("%d\n", Query(x));
        }
    }
}